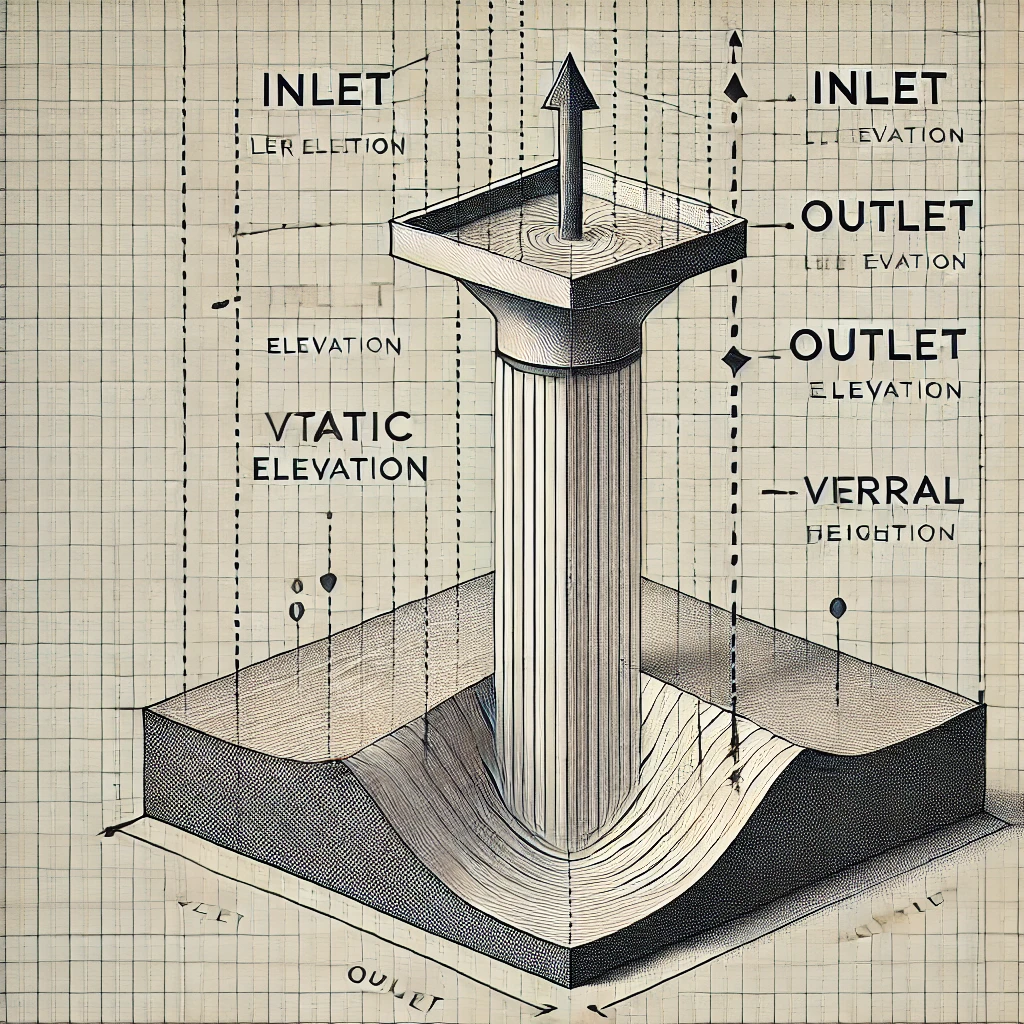
คำนวณความสูงที่น้ำต้องถูกยกขึ้น Static Head
Static Head คือความสูงที่น้ำต้องถูกยกขึ้นจากระดับเริ่มต้นถึงจุดปลายทาง โดยไม่คำนึงถึงแรงเสียดทานหรือแรงต้านอื่นๆ ที่เกิดขึ้นในระบบ
Static Head คำนวณจาก:
-
ความต่างระดับแนวดิ่ง (Vertical Elevation Difference):
โดย:
- คือ Static Head (หน่วย: เมตร หรือ ฟุต)
- คือระดับความสูงของปลายทางที่น้ำต้องถูกยกไป
- คือระดับความสูงของจุดเริ่มต้นของน้ำ
-
ในกรณีที่เป็นระบบแบบปิด:
ถ้าระบบมีแรงดันเริ่มต้นหรือปลายทาง (Pressure Head) คำนึงถึงแรงดันที่ต้องการด้วย:โดย:
- คือความต่างระดับแนวดิ่ง (Vertical Elevation Difference)
- คือแรงดันปลายทางและแรงดันเริ่มต้น (หน่วย: Pa)
- คือความหนาแน่นน้ำ (น้ำประปา: 9,800 N/m³)
ตัวอย่างการคำนวณ
-
กรณีไม่มีแรงดันเพิ่ม:
- จุดเริ่มต้น: เมตร
- จุดปลายทาง: เมตร
Static Head เมตร
-
กรณีระบบมีแรงดัน:
- จุดเริ่มต้นที่แรงดัน Pa
- จุดปลายแรงดัน Pa
- ความหนาแน่นของน้ำ
- ความต่างระดับแนวดิ่ง
คำนวณ:




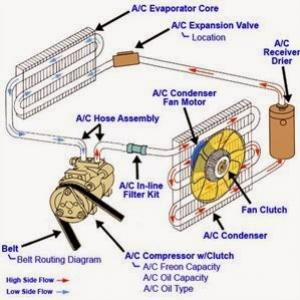





ระบบดับเพลิง